기울기와 접선과 미분 그리고 평균 기울기와 순간 기울기
2024. 11. 25. 14:22ㆍ경제 게임 만들기/그림으로 보는 수학
지난 글에서는 함수와 그래프에 대해 썼다.
이제 기울기와 접선과 미분에 대해 설명하겠다.
기울기는 지난글에도 잠깐 언급했는데, \( x \) 가 증가할 때, \( y \)가 얼마나 증가했는지 보는 것이다.

\( y = 2x \) 그래프에서 기울기는 2이다. \( x \)가 1 증가할 때 \( y \)는 2 증가한다.
그런데 기울기를 볼 때 어디서부터 어디까지 기준이 있을 것이다. 그리고 이게 평균 기울기다.
아래 그래프를 보자.

\( y = x^2 \)그래프는 직선이 아니다. 그래서 기울기는 측정 지점마다 달라진다. 아래 예시를 보자.

\( y = x^2 \)그래프를 따라 \( (0, 0) \) 에서 \( (1, 1) \) 로 이동할 때 평균 기울기는 1이다.

\( y = x^2 \)그래프를 따라 \( (0, 0) \) 에서 \( (2, 4) \) 로 이동할 때 평균 기울기는 2이다.

\( y = x^2 \)그래프를 따라 \( (1, 1) \) 에서 \( (2, 4) \) 로 이동할 때 평균 기울기는 2이다.

\( y = x^2 \)그래프를 따라 \( (-2, 4) \) 에서 \( (1, 1) \) 로 이동할 때 평균 기울기는 -1이다.
\( y = x^2 \)그래프를 따라 \( x \)가 1에서 1.01로 이동할 때 평균 기울기는 어떻게 될까?
\( y \)가 1에서 1.0201로 갔으니 평균기울기는 \( (1.0201 - 1) / (1.01 - 1) = 2.01 \) 이 될 것이다.
만약 \( x \)가 1에서 1.00001로 갈 때는 어떻게 될까?
\( y \)는 1에서 1.0000200001로 간다. 기울기는 2.00001 이다.
\( x \)가 1에서 \( x \)의 변화량이 작아질수록 기울기는 2에 근접한다.
이렇게 x의 변화량을 무한히 작게한 뒤 특정 지점에서의 기울기를 구하는 것이 순간 기울기이며, 이것을 수학적으로 구하는 방법이 미분이다. 미분하는 방법을 수식으로 표현하면 다음과 같다.
$$
f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}
$$
\( f(x) \)는 함수의 값이다. 함수에 \( x \)를 넣으면 나오는 값이란 뜻이다. 여기서 \( f(x) \)는 \( y \)와 같다할 것이다. 다시말해 \( y = x^2 \)이므로 \( f(x) = x^2 \)이다.
\( \displaystyle \lim_{\Delta x \to 0} \) 는 \( \Delta x \to 0 \)가 무한히 진행된다는 뜻이다. 다시 말해 \( x \)의 변화량이 끊임없이 0에 무한히 가까이 간다는 뜻이다. (참고로 수학에서 이렇게 변화량이 0에 근접하는 경우 변수 앞에 간단히 d를 앞에 붙여 표기하기도 한다.) 이렇게 구한 식을 $ f'(x) $ 처럼 작은 따옴표(')를 붙여 표기하고 도함수라 부른다. 다시 말해 $ f(x) $를 미분하면, 도함수 $ f'(x) $ 가 나온다.
이제 예시로 미분을 해보자.
$$
f(x) = x^2 \quad \text{일 때, 미분을 전개하면:}
$$
$$
f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}
$$
$$
= \lim_{\Delta x \to 0} \frac{(x + \Delta x)^2 - x^2}{\Delta x}
$$
$$
= \lim_{\Delta x \to 0} \frac{x^2 + 2x\Delta x + (\Delta x)^2 - x^2}{\Delta x}
$$
$$
= \lim_{\Delta x \to 0} \frac{2x\Delta x + (\Delta x)^2}{\Delta x}
$$
$$
= \lim_{\Delta x \to 0} \left( 2x + \Delta x \right)
$$
$$
= 2x
$$
어떤가. 천천히 생각해보면 미분은 별거 없다. 그저 독립변수에 매우작은 변화를 줄 때 종속변수는 얼마나 변하는지 보는 것이다. 생각보다 쉽다.
일반적인 함수로 확장해보자. (아래 식은 어려우면 재끼자)
$$
y = ax^b + c \quad \text{일 때, 미분을 전개하면:}
$$
1. 미분 정의에 대입:
$$
\frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}
$$
$$
= \lim_{\Delta x \to 0} \frac{[a(x + \Delta x)^b + c] - [ax^b + c]}{\Delta x}
$$
2. 상수 \( c \) 소거:
$$
= \lim_{\Delta x \to 0} \frac{a(x + \Delta x)^b - ax^b}{\Delta x}
$$
3. \( (x + \Delta x)^b \) 전개 (이항 정리 사용):
$$
(x + \Delta x)^b = x^b + b x^{b-1} \Delta x + \frac{b(b-1)}{2} x^{b-2} (\Delta x)^2 + \cdots
$$
따라서:
$$
\frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{a \left( x^b + b x^{b-1} \Delta x + \frac{b(b-1)}{2} x^{b-2} (\Delta x)^2 + \cdots \right) - ax^b}{\Delta x}
$$
4. 항목 정리:
$$
= \lim_{\Delta x \to 0} \frac{ax^b + abx^{b-1} \Delta x + \frac{ab(b-1)}{2} x^{b-2} (\Delta x)^2 + \cdots - ax^b}{\Delta x}
$$
5. \( ax^b \) 소거 및 \(\Delta x\)로 나누기:
$$
= \lim_{\Delta x \to 0} \frac{abx^{b-1} \Delta x + \frac{ab(b-1)}{2} x^{b-2} (\Delta x)^2 + \cdots}{\Delta x}
$$
$$
= \lim_{\Delta x \to 0} \left( abx^{b-1} + \frac{ab(b-1)}{2} x^{b-2} \Delta x + \cdots \right)
$$
6. \(\Delta x \to 0\) 적용:
$$
= abx^{b-1}
$$
최종 결과: 흔히 아는 미분공식이 나온다.
$$
\frac{dy}{dx} = abx^{b-1}
$$
그런데 미분의 값이 특정 지점에서의 순간 기울기인 것은 위 공식이 아닌 아까전의 예를 통해 쉽게 알 수 있었다.
그런데 순간 기울기(미분 값)가 접선의 기울기라고 한다. 왜 그런지 알아보자.


위 그래프를 보자. 왼쪽의 곡선 그래프를 특정 지점을 골라 상당히 확대를 해보면 오른쪽처럼 나온다.
멀리서 보면 곡선이였지만 매우 크게 보면 직선처럼 보인다. 지구는 둥글지만 표면에 있는 사람에겐 매우 확대되어 평평해으로 보이는 것과 같은 이치다.


이렇게 매우 확대해서 근사하면 기울기는 2가 된다.
그런데 접선이란 것이 무엇인가? 풀어쓰면 접하는 선이다. 어떤 곡선이 있으면 그 곡선에 접하는 선인 것이다. 그리고 이 접선은 곡선에서 딱 하나이다.
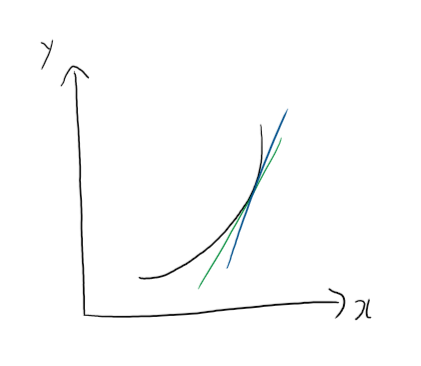
얼핏 곡선을 보면 접선이 여러 개가 있지 않을까 생각할 수 있다. 그런데 앞서 곡선을 확대해본 것을 떠올리면 그럴 수 없다는 것을 이미 알았을 것이다. 곡선을 무한히 확대해보면 직선에 근접한다. 그리고 이 직선은 딱 한개며, 이 직선이 그 점에서의 접선인 것이다.

접선의 기울기의 정의가 이러하니 당연히 접선의 기울기는 그 점에서의 순간 기울기가 된다.
다음에는 편미분에 대해 알아보자.
편미분의 이해
지난 글에서 미분에 대해 배웠다.다시 정리해보자면 미분은 원 함수의 기울기에 대한 함수를 구하는 것이다. 미분 값은 그 지점에서의 순간 기울기이다. 순간 기울기는 접선의 기울기이다. 그
heumdoneo.tistory.com
'경제 게임 만들기 > 그림으로 보는 수학' 카테고리의 다른 글
| 정적분과 부정적분 (0) | 2024.12.02 |
|---|---|
| 적분의 기초 이해 (1) | 2024.11.27 |
| 편미분의 이해 (0) | 2024.11.26 |
| 그래프의 이해 - 그래프 읽는 법과 함수 (0) | 2024.11.24 |
| 그래프의 이해 - 좌표평면, 직교 좌표계 (0) | 2024.11.23 |